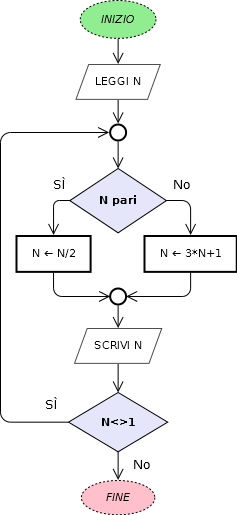
La congettura (probabilmente vera ma non ancora dimostrata) afferma che se si applica ripetutamente la formula seguente si giunge sempre al valore 1, indipendentemente dal valore di partenza (Wikipedia: Congettura di Collatz)
Ecco la sequenza che comincia da 17
| n | Pari/Dispari? | n’ |
| 17 | Dispari | 3*17+1=52 |
| 52 | Pari | 52/2=26 |
| 26 | Pari | 26/2=13 |
| 13 | Dispari | 3*13+1=40 |
| 40 | Pari | 40/2=20 |
| 20 | Pari | 20/2=10 |
| 10 | Pari | 10/2=5 |
| 5 | Dispari | 3*5+1=16 |
| 16 | Pari | 16/8=8 |
| 8 | Pari | 8/2=4 |
| 4 | Pari | 4/2=2 |
| 2 | Pari | 2/2=1 |
| 1 | STOP | |
Quando si arriva al valore 1 si interrompe l’esecuzione altrimenti si continuerebbe per sempre con 4 – 2 – 1 – 4 – 2 – 1 – …
Codice
TextWindow.Write("n = ")
n=TextWindow.ReadNumber()
While(n <> 1)
If(Math.Remainder(n,2) = 0) Then
n=n/2
Else
n=3*n+1
EndIf
EndWhile
TextWindow.WriteLine("Finito!")
Note
- Se Math.Remainder(n, 2) = 0 allora n è pari
- Se il ciclo While termina per ogni n allora la congettura è vera…
Aggiungi dei messaggi a schermo per evidenziare i passi del ciclo While
TextWindow.Write("n = ")
n=TextWindow.ReadNumber()
While(n <> 1)
TextWindow.Write(n + " -> ")
If(Math.Remainder(n,2) = 0) Then
n=n/2
Else
n=3*n+1
EndIf
TextWindow.WriteLine(n)
EndWhile