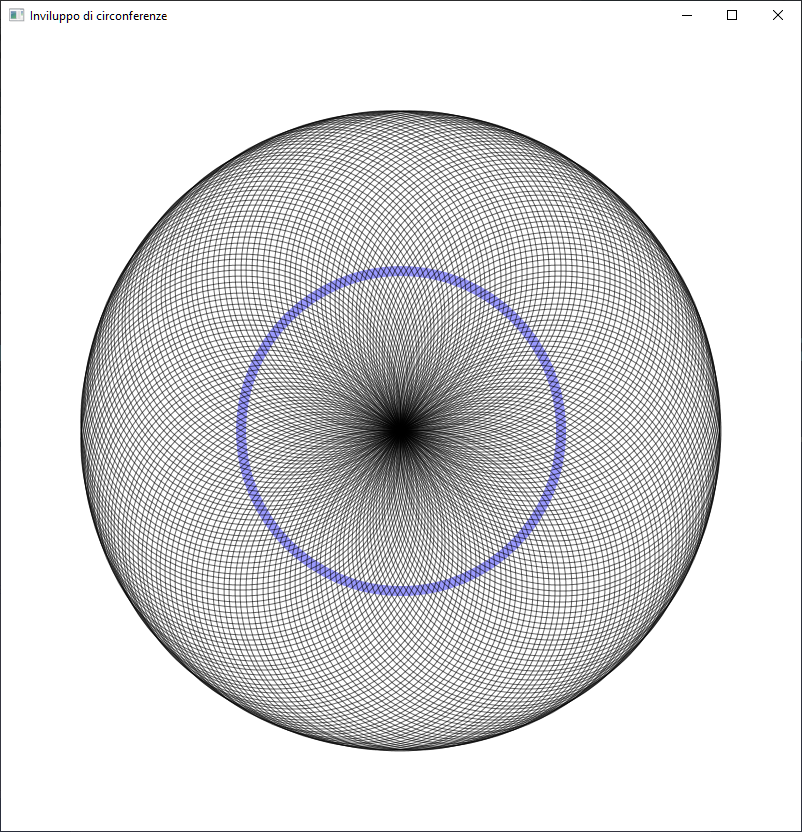
180 cerchi con centro sul cerchio blu e raggio costante

DIM =800 DIM2=DIM/2 GraphicsWindow.Title ="Inviluppo di circonferenze" GraphicsWindow.Width =DIM GraphicsWindow.Height=DIM xc=DIM2 yc=DIM2 n =180 angolo =0 angoloDelta=2*Math.Pi/n diametro1 =0.8*DIM diametro2 =2/3*diametro1 diametro3 =diametro1/3 raggio2 =diametro2/2 raggio3 =diametro3/2 GraphicsWindow.PenWidth=10 GraphicsWindow.PenColor="#660000FF" GraphicsWindow.DrawEllipse(xc-raggio2,yc-raggio2, diametro2,diametro2) GraphicsWindow.PenWidth=1 GraphicsWindow.PenColor="#99000000" For i=1 To n x=xc+raggio2*Math.Cos(angolo) y=yc-raggio2*Math.Sin(angolo) GraphicsWindow.DrawEllipse(x-raggio3,y-raggio3, diametro3,diametro3) angolo=angolo+angoloDelta Program.Delay(25) EndFor
Con diametri e raggi diversi
diametro1=0.8*DIM diametro2=diametro1/2 diametro3=diametro2 raggio2 =diametro2/2 raggio3 =diametro3/2
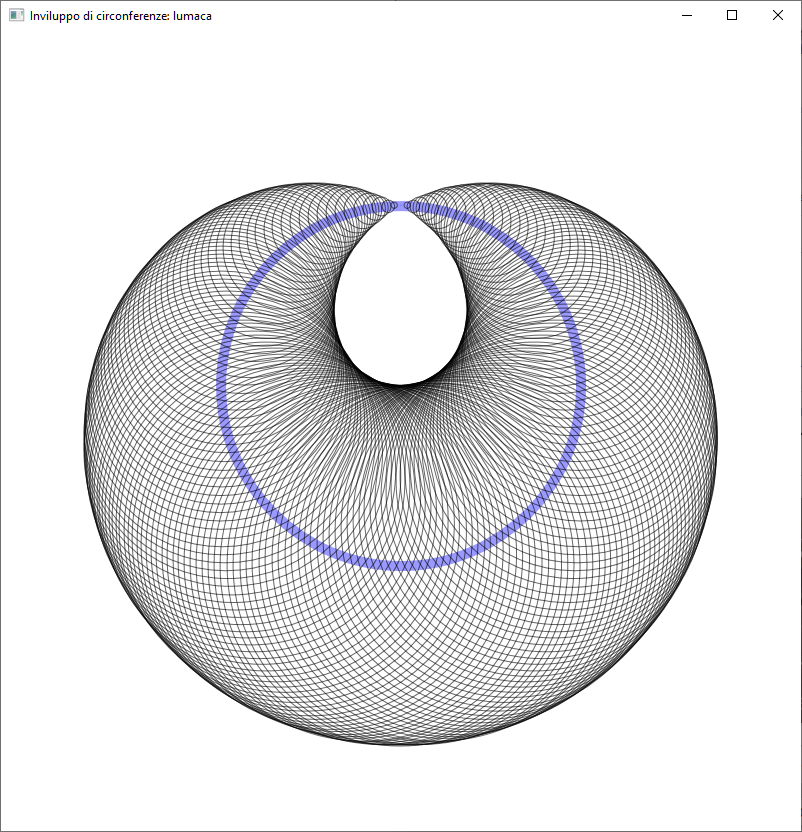
Cardioide
Il raggio è dato dalla distanza tra il punto sulla circonferenza blu e il punto fisso in alto al centro

Lumaca di Pascal
Il raggio è la metà della distanza da …
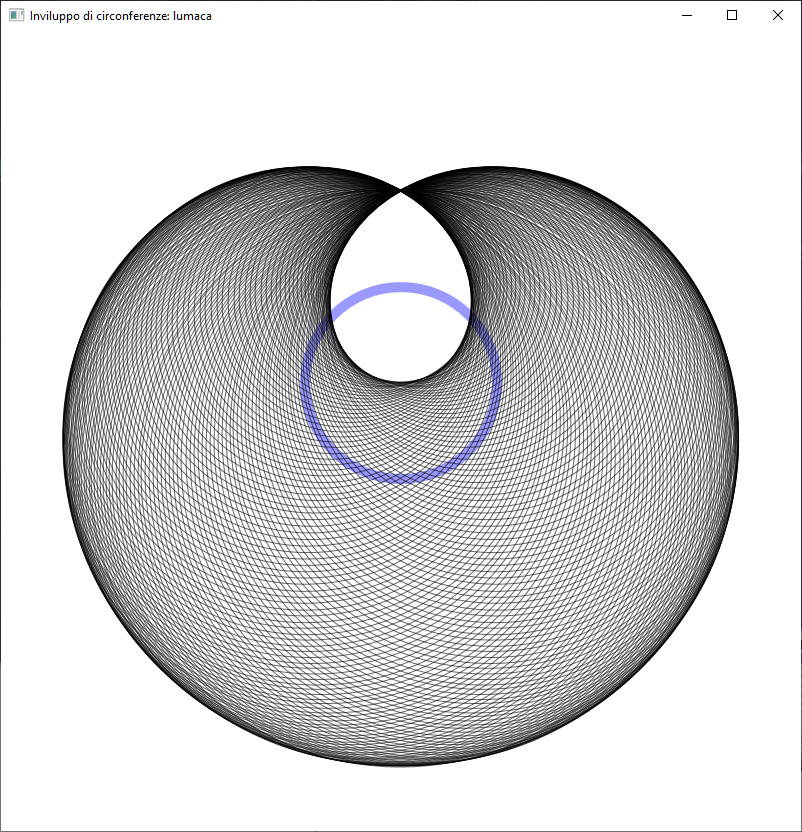
La stessa figura ma con il cerchio blu più piccolo e il punto focale più lontano
Nefroide
Il raggio è dato dalla distanza dall’asse centrale

DIM =800 DIM2=DIM/2 GraphicsWindow.Title ="Inviluppo di circonferenze: nefroide" GraphicsWindow.Width =DIM GraphicsWindow.Height=DIM n =180 angolo=0 angoloDelta=2*Math.Pi/n diametro1 =0.8*DIM diametro2 =diametro1/2 raggio2 =diametro2/2 xc=DIM2 yc=DIM2 GraphicsWindow.PenWidth=10 GraphicsWindow.PenColor="#660000FF" GraphicsWindow.DrawEllipse(xc-raggio2,yc-raggio2, diametro2,diametro2) GraphicsWindow.PenWidth=1 GraphicsWindow.PenColor="#99000000" For i=1 To n x=xc+raggio2*Math.Cos(angolo) y=yc-raggio2*Math.Sin(angolo) raggio3=Math.abs(x-xc) diametro3=2*raggio3 GraphicsWindow.DrawEllipse(x-raggio3,y-raggio3, diametro3,diametro3) angolo=angolo+angoloDelta Program.Delay(25) EndFor
La curva blu può essere una parabola, un’iperbole